普通の電卓で計算できる直角三角形の近似計算
はじめに
三角形の中でも最も便利な三角形に直角三角形があります。
中学校では、直角三角形の3つの辺の長さを結びつける「三平方の定理」 (ピタゴラスの定理ともいう)を習いますが、三角形の角度と辺の長さを 結びつけるものはどうでしょうか。
中学校では30°、45°、60°の角度と辺の関係しか習いません。 高校では三角関数というものを習いますので、それを使って式で表すことは 出来るようになりますが、数字で値を出すには特別な電卓や表を使わないと いけません。
でも、大学で習うちょっとした方法を使うと普通の電卓でも、 角度と辺の関係を数字で出すことができます。 ここでは、その使い方だけを説明したいと思います。
ここで紹介する方法では、細かい数字が出るところを無視してしまって いるのでぴったりな数字を出すことは出来ませんが、 それでもあなたがちょっとした問題を解決するためには、十分に役立つはずです。
具体的に言うと、ここでは角度が小さいとき(0~45°)のsin(サイン)と arcsin(アークサイン)の近似式を紹介しています。
用意するもの
- 平方根(√)が計算できる電卓。
- メモ用の紙とペン。
- 中学生程度の数学的基礎。
準備1.三角形のおやくそく
これから考える三角形を約束します。
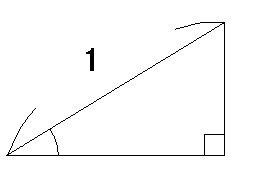
- 直角三角形である
- 直角であるカドの反対側にある辺の長さは1である
三角形の大きさを変えるときは、相似の三角形を考えて計算できますね。
準備2.角度の表し方
普段使う角度は一周を360°として等間隔に目盛りをふって決めています。 たとえば、一周の半分は360°の半分で180°になりますね。
一周が360°というのは目盛りを360個ふっておくと、2人、3人、4人、5人、 6人、8人、9人、10人、12人、15人、18人、20人、24人、30人、36人、 40人、45人、60人、72人、90人、120人、180人、360人でケーキを分けるとき ケンカにならずにとっても便利だからです。
このような方法は度数法(どすうほう)と呼ばれるものなのですが、 角度を表すには弧度法(こどほう)という別の方法もあります。
弧度法は、半径が1の円を表したい角度で切り取った「おうぎ形」の弧の長さを 使ってあらわすもので、度数法から弧度法に直すのは弧の長さの比から 次の式で簡単にできます。
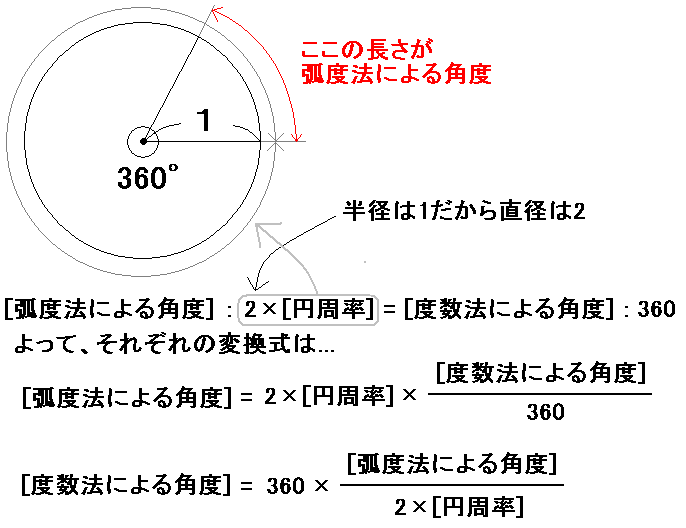
ここで使う角度はすべて弧度法なので覚えておいてください。
基本.直角三角形の角度とその角の反対にある辺の長さ(0~45°)…サインの近似(sinの近似)
では、いよいよ角度と辺の長さの関係を式で表してみましょう。
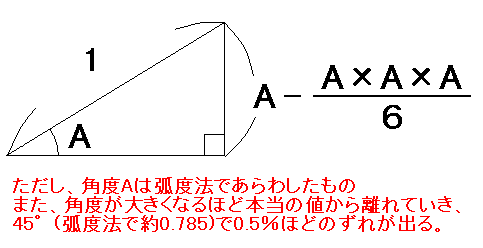
三平方の定理と三角形の内角の和の関係を知っていれば新しく覚えるのは これだけです。
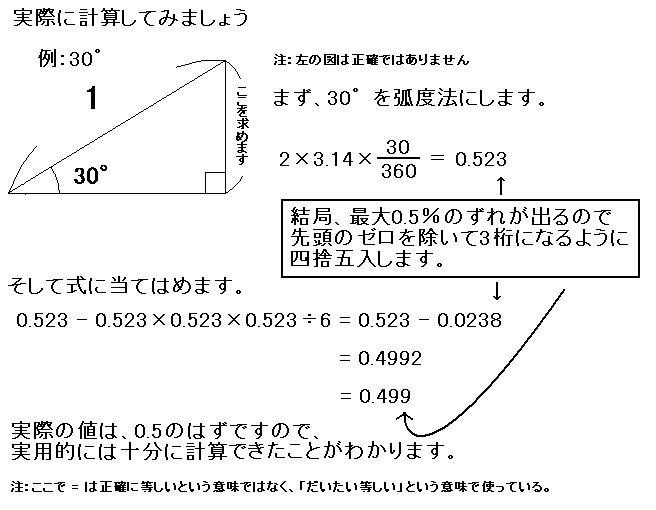
ちょっと進んだ話
興味のある人向けになんでこうなるのかをもう少しだけ説明します。
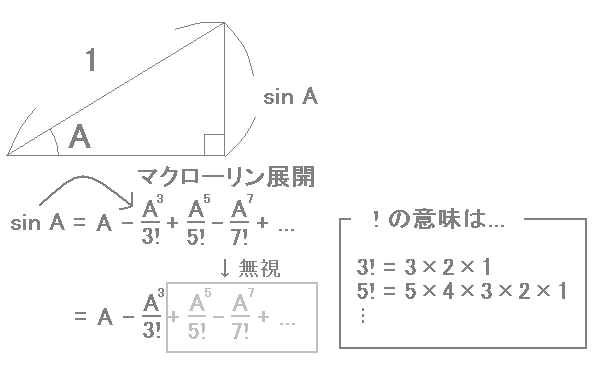
この関係は、高校で習う三角関数を使うとsin関数を使ってあらわすことが できます。さらに、弧度法を使って角度を表すと、大学で習う「マクローリン展開」 と呼ばれる方法を使って限りなく続く多項式であらわすことが出来ます。
さて、ここで分母がどんどん大きくなっていること、さらに弧度法で表した 角度が1より小さければ、3乗、5乗していくと分子がどんどん小さくなっていく ことに注目します。
45°を弧度法で表すと (半径1の円周の長さ)×(45°の360°に対する割合)=(2×3.14)×(45÷360)=0.785 です。 このことを考えると5乗以上の項は無視できると考えることができます。
そうしたわけで、上の式で表すことが出来るとなったのです。
応用1.直角三角形の角度とその角の反対にある辺の長さ(45~90°)
さて、この方法では角度が大きくなるにしたがってどんどん本当の値から 離れていってしまいます。 (たとえば、60°では1%強の差、80°では4%強の差が出てしまいます。)
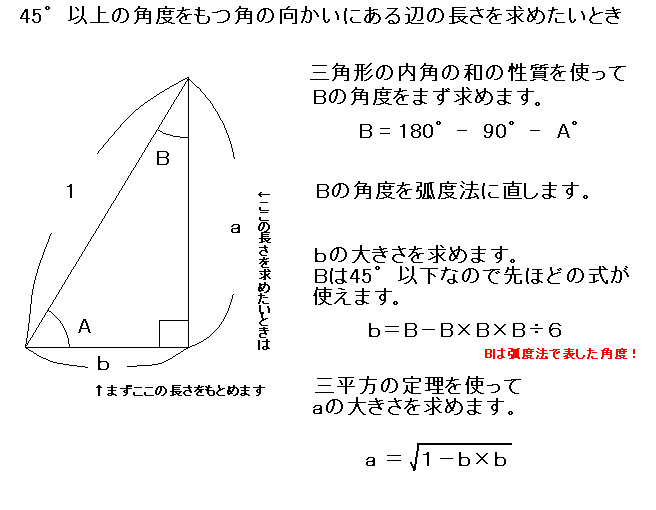
でも、45°までの計算を覚えたら、ちょっと工夫することで 45°以上の角度でも問題なくこの式を使って計算することが出来るように なります。どうすれば良いでしょうか。ヒントは45°以上の角度を45°以下の 角度であらわせばよいということです。
わかりましたか?三角形の3つの角の角度の和は180°ということを使えば 直角でないもう一方の45°以下である角度を求めることが出来ますね。 そして、それをつかって長さを求めたい辺に直角でくっついている辺の長さを 求めます。そして、三平方の定理(ピタゴラスの定理)をつかって 求めたい辺の長さを求めればいいのです。
応用2.分度器を使わずにすきな角度を作る
「手元に分度器が無いけれど、どうしてもある角度がどのくらいか知りたいんだ!」 というときはどうすれば良いでしょうか。そんなことはめったに無いかもしれませんが ちょっと考えて書いてみましょう。 分度器がなくても「ものさし」と「直角」はなんとか用意してください。
このときも、基本の三角形で考えます。まず、書きたい角度の反対側にある 辺の長さを求めます。もし、書きたい角度が45°以上ならば、もう一方の直角でない角を 使って辺の長さを計算してください。
つぎに、三平方の定理を使ってもう一方の辺の長さを計算します。
最後に直角をはさんで、これらの2つの辺の長さの比を持つ三角形を 書けば知りたい角度を書くことが出来ます。
応用3.直角三角形の二つの辺の長さから角度を求める…アークサインの近似(asinの近似)
1つ上の応用よりこっちのほうが実用的かもしれません。ちょっとした裏技を 使いますが、式に当てはめれば大丈夫です。
まず、三平方の定理を使って2つの辺からもう1つの辺の長さを計算します。
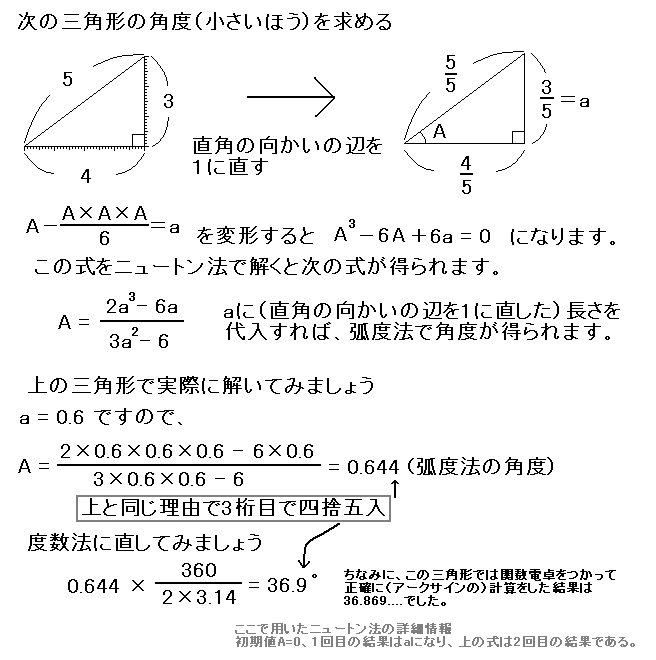
それから、直角の反対側にある辺の長さが1になるような相似の三角形を考え、 直角をはさんでいる2つの辺の長さのうち短いほうを選びます。これは、 約束の三角形に直して、45°以下の角を選ぶためです。
この値を始めに紹介した式に代入すれば三次方程式になります。 ここで「三次方程式の解の公式」を使って答えを求めることも出来ますが、 この公式は3乗根(√の3乗版)を使わなければいけません。 これでは、一般的な電卓で計算することはできません。
いろいろ考えましたが、コンピュータを使った計算で用いられる 「ニュートン法」を使う方法がよさそうです。 式の形がちょうどニュートン法できれいな形になるようになっていました。 ただし、「ニュートン法」も正確な値を出せるものではありません。
もう一方の角度は三角形の内角の和の関係をつかって求めることができます。
この方法でもやはり角度が0から大きくなると本当の値から離れていきますが、 表計算ソフトでざっと計算したところ0~45°の範囲では 最大約0.026°(約41°の時)の差が発生するようです。 45°の時でなかったのはA-A×A×A÷6で発生した差と うまい具合に打ち消しあったからでしょう。
上記の方法を応用すれば、アークタンジェント(atan)やアークコサインと呼ばれる関数の答えも近似計算できますね。
応用4.あなたしだい
補助線を引けばいろいろな図形をこの方法で解いたり書いたりする ことが出来ます。いろいろと考えてみましょう。
忘れてはいけないのは、 0~45°までしかA-A×A×A÷6の式は使えない!Aに代入する角度は弧度法! ということです。それでも、直角三角形ならば上記のような工夫をすることで、 実用上は問題なく計算出来るようになります。 簡単な式ですから、覚えておくといつの日か使えるかもしれません。
まだまだわかりにくい所もあるかもしれませんが、その点はお許しください。
2007年3月25日 2007年春休み企画
2020年4月24日 新型コロナ渦中にちょっと加筆